Response to a question
Response to a question¶
Q. In the derivation of the momentum theory, the momentum conservation equation was applied as T = rate of change of momentum = (final momentum - initial momentum) / t; applying this between stations 0 and 2 in the slipstream leads to the following
and not,
as was derived in the lecture. Which is the right equation? Why?
The derivation shown in the lecture notes used the following equations applying the balance laws -
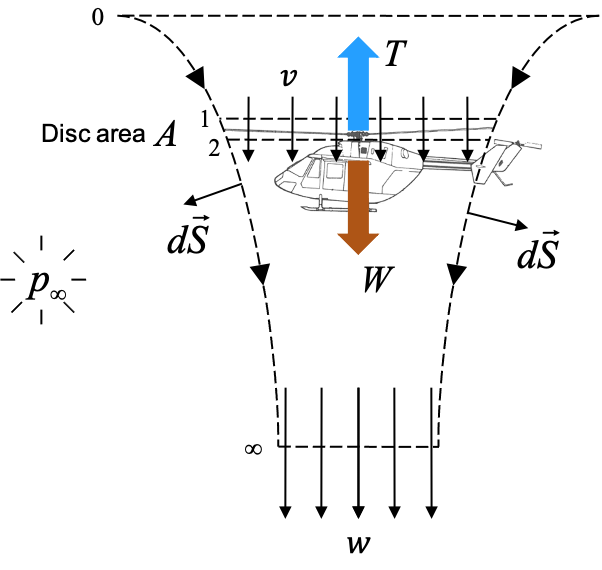
Hovering rotor flowfield model in momentum theory
Mass Conservation:$\( \dot{m} = \rho A v = \rho A_{\infty} w \)\( Momentum Conservation: \)\( T = \dot{m}w = (\rho A v) w \)\( Energy Conservation: \)\( T v = \frac{1}{2} \dot{m} w^2\)$
The question raised above can be framed in the context of the energy balance equation as well. The following explains why the equations used in the lecture are correct.
Fluid pressure works as a push rather than a pull. As work is done by the rotor, i.e. it increases pressure at station 2 within the actuator disk-based momentum theory model, the fluid can exchange that pressure increase for kinetic energy. This is the Bernoulli’s principle where the pressure can be thought of as a potential energy of the flow that can be exchanged for kinetic energy, and vice versa. This exchange occurs without any losses within the framework of the assumptions that the Bernoulli’s equation is based on -
So, high static pressure at station 2 and low static pressure at station \(\infty\) (atmospheric pressure) is going to set the direction of the flow within the stream tube. Fluid from station 1, and in turn from station 0, is set in motion since fluids are continuous and shocks do not occur at the low subsonic speeds that arise in VTOL rotor flows. Since all the work, and by extension the static pressure increase, is assumed to be confined to the thin actuator disk, the movement of flow from station 0 to station 1 occurs by exchanging some of the static pressure to dynamic pressure. The result is that the rate flow of momentum at the actuator disk becomes \((\rho vA)v\). However, static pressure calculation using Bernoulli’s equation show that there is an additional pressure of \(\frac{3}{4}\frac{T}{A}\) at station 2. This provides an additional upwards push and in turn adds to the overall thrust that the rotor is generating. The external work done by the rotor is not just an increase in fluid momentum, the potential energy (i.e. the static pressure) of the fluid is changed as well and needs to be accounted for to get an accurate estimate of the reaction force vector (i.e. thrust). Using the relation \( T = \dot{m}w = (\rho A v) w \) avoids that because the stations where the final and the initial momentums are considered are where the static pressure is the same (and therefore no unaccounted for energy storage).
The flow can be assumed to be incompressible throught the exercise since the Mach number never exceeds \(M=0.3\) at any point within the streamtube for conventional lifting rotors (this may not necessarily be true for jet exhaust in the case of the F35 or the Harrier jump-jet).
In order to convince yourself further about this, the following literature can be referred - [Sen14] (Pg 21-23) and [Bat00] (Pg 156).
